Redheffer and Mertens, Continued - Cleve Moler on Mathematics and Computing

[poster]

Shortly after I posted Redheffer, Mertens and One-Million Dollars a few days ago, Mathworks' Pat Quillen made an important observation about computing the Mertens function.

Contents

• mertens
• Mertens function
• Mertens computation
• Mertens conjecture

mertens

The elements in the first column of the Redheffer matrix, A = redheffer(n), are all equal to one. That dense column does not make MATLAB happy about computing det(A) . However, the last column of A has only a few nonzero elements and so Pat suggested interchanging the first and last columns before computing the determinant. This makes a world of difference. (Thanks, Pat.)

typemertensfunction M = mertens(n) if n > 1 A = redheffer(n); A(:,[1 n]) = A(:,[n 1]); M = -round(det(A)); else M = 1; endendThe time required to compute det(A) varies with the sparsity of the last column, but it is only a little more than the time to compute redheffer(n) in the first place.

mertens2_time 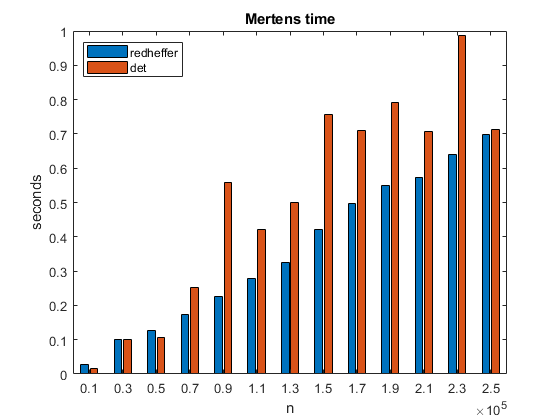Mertens function

Pat's change makes it possible to take n up to a quarter of a million, and beyond. Here is a new plot of the Mertens function M(n) and the sqrt(n) bounds of the Mertens conjecture.

mertens_plot 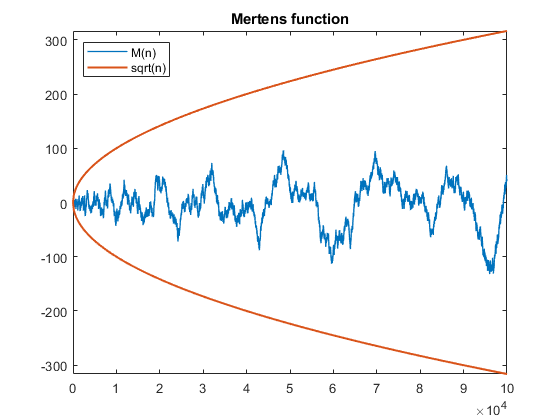There are a quarter of a million points in the data for this plot. Fortunately, the .PNG file used for the blog only needs to sample the data.

Mertens computation

The job that I ran on my laptop to compute one-quarter of a million values of M(n) is still running. It currently is past 0.35 million and takes less than two seconds for each value. I may keep the job running over the weekend, just to see how far it gets.

The task is embarrassingly parallel. If I had a pool with a million processors, I could have each processor compute one value. I would then just have to collect the results, but that doesn't involve any arithmetic.

Mertens conjecture

You can see from the plot why late 19th- and early 20th-century mathematicians believed that the Mertens conjecture,

|M(n)| < sqrt(n) for all n,might be true. It is hard to imagine that the plot of M(n) ever escapes sqrt(n).

We now know that M(n) eventually does escape, but only barely and only briefly. We also know that all the computation we can do with determinants of Redheffer's matrix will never prove or disprove the conjecture or win that million-dollar prize.

Get the MATLAB code (requires JavaScript)

Published with MATLAB® R2024a

More...