| Labfans是一个针对大学生、工程师和科研工作者的技术社区。 | 论坛首页 | 联系我们(Contact Us) |
 |
| Labfans是一个针对大学生、工程师和科研工作者的技术社区。 | 论坛首页 | 联系我们(Contact Us) |
 |
|
|
#1 |
|
高级会员
注册日期: 2019-11-21
帖子: 3,017
声望力: 67  |
LUTool provides an interactive animation of Gaussian elimination, the most important algorithm in technical computing.
Contents
The triangular factorization of a square, n-by-n matrix A is A(p,q) = L*Uwhere L is a lower triangular matrix with ones on the diagonal, U is an upper triangular matrix, and p and q are indices of row and column permutations. There are three kinds of pivoting. * none. No interchanges.* partial. Choose the largest element in the current pivot column.* complete. Choose the largest element in the entire unreduced matrix.In general, pivoting permutations are necessary for numerical stability by avoiding divisions by small pivots. However, some test matrices can be successfully factored without pivoting. LUTool LUTool displays the lower portion of L and the row indices p in blue and the upper portion of U and the column indices q in lavender. The product of the pivot values on the diagonal of U is the determinant of A. A popup menu lists the available test matrix families from gallery and from the MATLAB path. info and help buttons display information about the selected family and about LUTool itself. 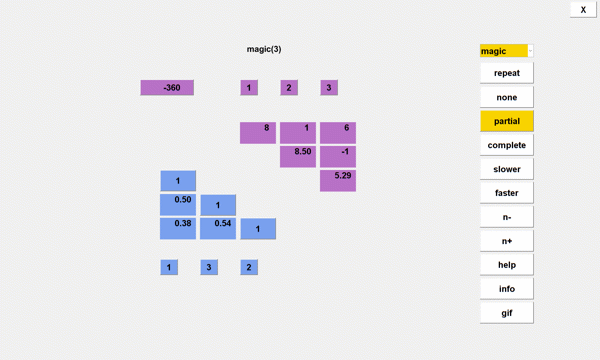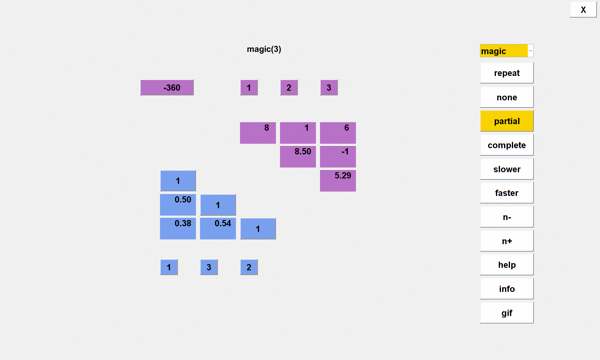 Magic Squares Here are the three pivoting options with the 5-by-5 magic square. complete  partial  none  Positive Definite Matrices Pascal matrices are positive definite and do not require pivoting. The same triangular factorization is computed by chol.  Redheffer Matrices Last fall, I made a series of blog posts about Redheffer matrices and the Riemann hypothesis. Since the first column of a Redheffer matrix is all ones, the resulting lower triangular factor is nearly full.  Pat Quillen suggested interchanging the first and last columns, so there would be much less fill-in.  Singular Matrices It is widely believed that only nonsingular matrices have triangular factorizations. However, with proper pivoting, singular matrices also have LU factorizations. (The consequences of singularity or poor conditioning are realized when U is subsequently used to solve a linear system.) For example, restart the random number generator with rng(1)Then n = 6 gallery('rando',n,0)produces a singular matrix and [A,p,q,L,U] = LUTool('rando',n,'partial',0.02)encounters two zero pivots. Nevertheless, the output satisfies A(p,q) = L*U  For my final example, the rank of the 8-by-8 magic square is only 3. LUTool with partial pivoting encounters five negligible pivots. The first three columns of L and the first three rows of U are all that is required to reconstruct the original magic square.  Software A self-extracting archive of LUTool is available from this link More... |
|
|

|