Redheffer, Mertens and One-Million Dollars - Cleve Moler on Mathematics and Computing

[poster]

I didn't know anything about these topics until a couple of weeks ago. Now I can't stop thinking about them.

• Redheffer's matrix has been in the MATLAB Gallery for a long time, but I have ignored it .
• Redheffer's matrix can be used to compute Mertens function and investigate the Mertens conjecture.
• A proof of the Mertens conjecture would also provide a proof of the Riemann hypothesis.
• For nearly a century, all the available computational evidence indicated that the Mertens conjecture was likely to be true.
• The Riemann hypothesis is the most important unsolved problem in mathematics and wins a Clay prize worth one-million dollars.
• MATLAB's sparse matrix functions turn out to be useful in an investigation of Redheffer's matrix and the Mertens conjecture.
• However, it has been known since 1985 that the Mertens conjecture is false.

Contents

• Redheffer's Matrix
• Möbius Function
• Mertens Function
• Mertens Conjecture
• Mertens Meets Redheffer
• Redheffer Sparsity
• redheffer
• Sparse LU
• mertens
• Mertens Conjecture Is False
• Postscripts
• References

Redheffer's Matrix

Raymond Redheffer (1921-2005) was an American mathematician, a professor at UCLA for 55 years, the author of several popular textbooks, the inventor of the electronic game Nim and, with Ray and Charles Eames, the creator of a four-meter long poster Men of Modern Mathematics.

Redheffer's matrix is a matrix of zeros and ones. A(k,j) equals one if j is a divisor of k. In addition, the first column is all ones.

function A = redheffer(n) k = 1:n; j = k'; A = (mod(k,j) == 0); A(:,1) = 1; endOr

A = gallery('redheff',n)Here is the 10-by-10.

A = redheffer(10); disp(full(A)) 1 1 1 1 1 1 1 1 1 1 1 1 0 1 0 1 0 1 0 1 1 0 1 0 0 1 0 0 1 0 1 0 0 1 0 0 0 1 0 0 1 0 0 0 1 0 0 0 0 1 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 1And here is a spy plot of the 200-by-200.

A = redheffer(200); spy(A) title('redheffer(200)') 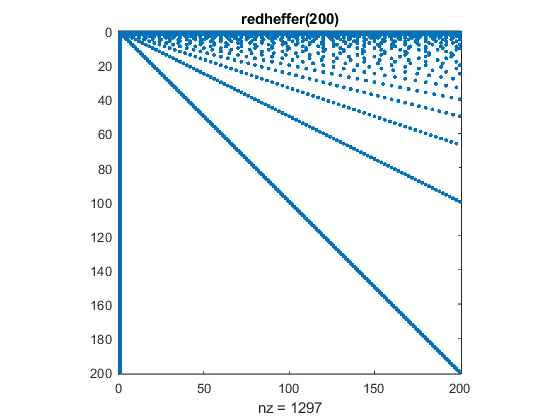Möbius Function

The Möbius function was introduced in 1832 by German mathematician August Möbius and is ubiquitous in the study of prime numbers. For positive integers n, μ(n) is

• 0 if n has a squared prime factor,
• +1 if n is square-free and has an even number of prime factors,
• -1 if n is square-free and has an odd number of prime factors.

Mertens Function

Franz Mertens (1840-1927) was a Polish mathematician who spent most of his career in Austria at the University of Vienna. Here is a link to a biography of Mertens at the University of St. Andrews MacTutor project.

The Mertens function is sum of values of the Möbius function. For a positive integer n, the Mertens function is

M(n) = sum(μ(1:n))So M(n) is the difference between the number of square-free integers with an even number of prime factors and those with an odd number.

This graphic shows M(n) for n = 1:100000.

mertens_plot_2 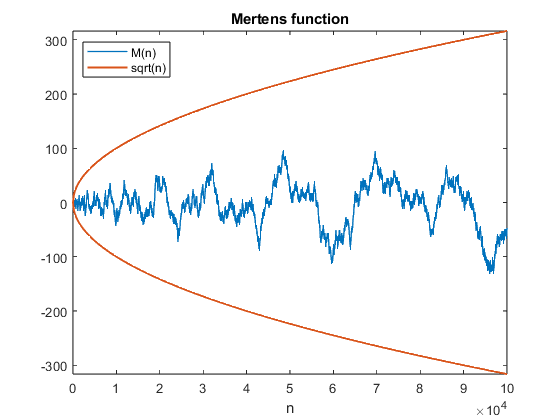Mertens Conjecture

The Mertens function M(n) fluctuates wildly and grows slowly with increasing n. The graphic shows that M(n) is easily bounded by of sqrt(n) and -sqrt(n), at least for n less than 100k. The Mertens conjecture is that this continues for larger n.

-sqrt(n) < M(n) < sqrt(n) for all nThe conjecture was included in a letter from Stieltjes to Hermite in 1895 and in a paper by Mertens in 1897. The result is important since a proof of the Mertens conjecture would imply the truth of the Riemann hypothesis.

Mertens Meets Redheffer

I became interested in all this when I learned that the determinant of the MATLAB Gallery matrix which I have ignored for years is related to the Riemann hypothesis and the million-dollar prize.

M(n) = det(gallery('redheff',n))I know very little about the distribution of prime numbers and computing values of the Möbius function. On the other hand, I know a lot about numerical linear algebra and computing determinants.

In general, I am dead set against computing determinants. They are often used to check for singularity or to somehow compute eigenvalues. But here the determinant is an integer counter of modest size.

Redheffer Sparsity

Computing M(n) directly with det(redheffer(n)) requires O(n^2) space and O(n^3) time and is not practical for large n.

However, A = redheffer(n) is modestly sparse. Here is the fraction of nonzeros.

s = nnz(A)/n^2 disp(sparsity) n s _____ ________ 10000 0.001037 20000 0.000553 30000 0.000382 40000 0.000294 50000 0.000239 60000 0.000203 70000 0.000176 80000 0.000156 90000 0.000139 1e+05 0.000127Taking advantage of this sparsity and the MATLAB tools for sparse matrix computation provide linear space complexity and perhaps O(n^2) time complexity.

redheffer

Here is MATLAB code to generate a sparse redheffer(n) without creating any full intermediate matrices.

type redheffer function A = redheffer(n) j(1:n) = (1:n)'; k(1:n) = 1; m = n; for i = 2:n t = [1 i:i:n]'; p = length(t); j(m+(1:p)) = t; k(m+(1:p)) = i; m = m+p; end A = sparse(k,j,1,n,n); endAs expected, we see that the execution time for redheffer(n) is a linear function of n. (The space required also grows linearly.)

redheffer_time 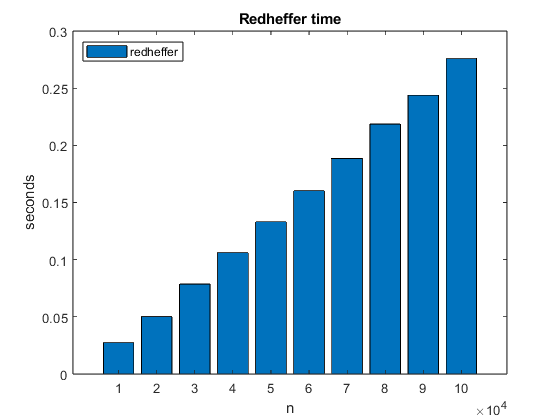Sparse LU

The MATLAB Gaussian elimination function lu with one sparse input and four sparse outputs is designed for solving sparse linear systems.

[L,U,P,Q] = lu(A)Written primarily by Tim Davis and included in his UMFPACK package, the function uses an unsymmetric pattern multifrontal pivoting strategy to find permutations P and Q so that L is lower triangular, U is upper triangular and

P*A*Q = L*UConsequently, the determinant of A is the product of four easily computed determinants.

det(A) = det(L)*det(U)*det(P)*det(Q)The pivoting strategy aims to reduce fill-in while maintaining numerical stability.

For example, here are L and U for the Redheffer matrix in the spy plot near the top of this blog post.

close A = redheffer(200); [L,U,P,Q] = lu(A); spy(L|U) title('L|U') 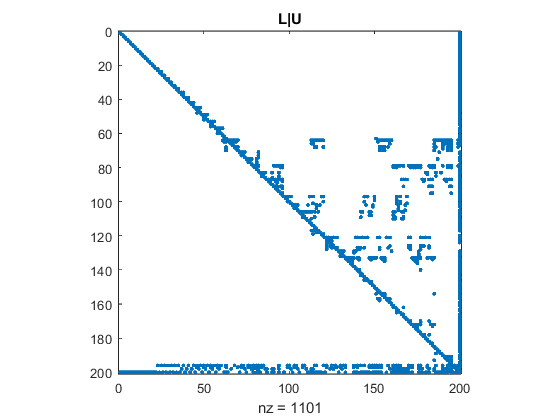And here are the four determinants.

dets = [det(L),det(U),det(P),det(Q)]; disp(dets) 1 -8 -1 -1Finally, M(200) is

M_200 = det(L)*det(U)*det(P)*det(Q) M_200 = -8mertens

Mertens function can be computed with four lines of code.

type mertens function M = mertens(n) der = @(x) full(round(prod(diag(x)))); A = redheffer(n); [L,U,P,Q] = lu(A); M = der(L)*der(U)*det(P)*det(Q); endExecution time for mertens is dominated by the time in sparse lu. The time required to compute the four determinants is an order of magnitude smaller than the other two.

Experimentally, we see that the time complexity of sparse lu is O(n^2), but we have no proof.

mertens_time 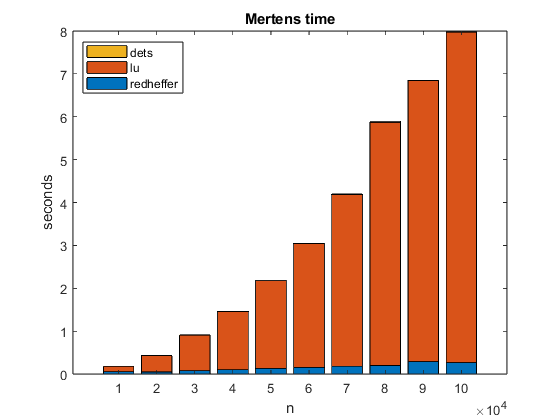Mertens Conjecture Is False

The Mertens conjecture stood for nearly 100 years before it was proved false in 1985 by Andrew Odlyzko and Herman te Riele. The authors present indirect proofs that

lim sup (n -> inf) M(n)/sqrt(n) > 1.06 lim inf (n -> inf) M(n)/sqrt(n) < -1.009Odlyzko and te Riele do not actually produce any value of n for which M(n) > sqrt(x). They suspect that any Mertens conjecture counterexample requires n > $10^{30}$, which is far beyond any computation possible today.

Odlyzko and te Riele also describe several complete tabulations of M(n) for n as large as $7.8 \cdot 10^{9}$ . These computations do not use Redheffer determinants.

Postscripts

To tell the truth, I did not really expect to find any Mertens or Riemann counterexamples. I did, however, enjoy computing determinants for the first time and discovering an unexpected use for sparse LU.

Thanks a lot to Tim Davis for his help with this post.

References

A. M. Odlyzko and H. J. J. te Riele, "Disproof of the Mertens conjecture", Journal für die reine und angewandte Mathematik, Vol. 357 (1985), Pages138-160. https://eudml.org/doc/152712.

Timothy A. Davis, "A Column Pre-Ordering Strategy for the Unsymmetric-Pattern Multifrontal Method", ACM Transactions on Mathematical Software, Vol. 30, No. 2, June 2004, Pages 165–195. https://dl.acm.org/doi/abs/10.1145/992200.992205.

Get the MATLAB code (requires JavaScript)

Published with MATLAB® R2024a