My colleagues are looking for a matrix to be used in a new benchmark. They've come to the right place.
Contents
Email
A couple of weeks ago I got this email from Jack Dongarra at the University of Tennessee.
For this new HPL-AI benchmark, I'm looking for a matrix that is not symmetric, is easily generated (roughly O(n^2) ops to generate), is dense, doesn’t require pivoting to control growth, and has a smallish condition number ( -1, the largest element is on the diagonal and lu(A(n,mu)) does no pivoting.
format short mu = -1 [L,U] = lu(A(n,mu)) mu = 1 [L,U] = lu(A(n,mu)) mu = -1 L = 1.0000 0 0 0 0 0.2083 1.0000 0 0 0 0.2778 0.1748 1.0000 0 0 0.4167 0.2265 0.1403 1.0000 0 0.8333 0.3099 0.1512 0.0839 1.0000 U = 1.2000 0.1667 0.1429 0.1250 0.1111 0 1.1653 0.1369 0.1168 0.1019 0 0 1.1364 0.1115 0.0942 0 0 0 1.1058 0.0841 0 0 0 0 1.0545 mu = 1 L = 1.0000 0 0 0 0 0.1094 1.0000 0 0 0 0.0972 0.0800 1.0000 0 0 0.0875 0.0729 0.0626 1.0000 0 0.0795 0.0669 0.0580 0.0513 1.0000 U = 1.1429 0.1250 0.1111 0.1000 0.0909 0 1.0974 0.0878 0.0800 0.0734 0 0 1.0731 0.0672 0.0622 0 0 0 1.0581 0.0542 0 0 0 0 1.0481
Condition
Let's see how the 2-condition number, $\sigma_1/\sigma_n$, varies as the parameters vary. Computing the singular values for all the matrices in the following plots takes a little over 10 minutes on my laptop.
sigma_1
load HPLAI.mat s1 sn n mu surf(mu,n,s1) view(25,12) xlabel('mu') ylabel('n') set(gca,'xlim',[-0.9 1.0], ... 'xtick',[-0.9 -0.5 0 0.5 1.0], ... 'ylim',[0 2500]) title('\sigma_1')

The colors vary as mu varies from -0.9 up to 1.0. I am staying away from mu = -1.0 where the matrix looses diagonal dominance. The other horizontal axis is the matrix order n. I have limited n to 2500 in these experiments.
The point to be made is that if mu > -0.9, then the largest singular value is bounded, in fact sigma_1 < 2.3.
sigma_n
surf(mu,n,sn) view(25,12) xlabel('mu') ylabel('n') set(gca,'xlim',[-0.9 1.0], ... 'xtick',[-0.9 -0.5 0 0.5 1.0], ... 'ylim',[0 2500]) title('\sigma_n')
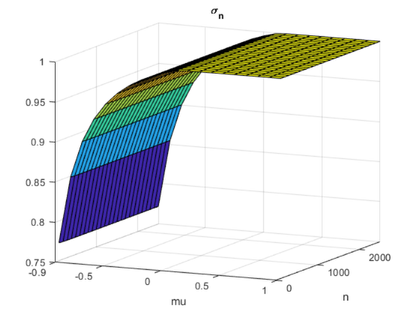
If mu > -0.9, then the smallest singular value is bounded away from zero, in fact sigma_n > .75.
sigma_1/sigma_n
surf(mu,n,s1./sn) view(25,12) xlabel('mu') ylabel('n') set(gca,'xlim',[-0.9 1.0], ... 'xtick',[-0.9 -0.5 0 0.5 1.0], ... 'ylim',[0 2500]) title('\sigma_1/\sigma_n')

If mu > -0.9, then the condition number in the 2-norm is bounded, sigma_1/sigma_n < 2.3/.75 $\approx$ 3.0 .
Overflow
The HPL-AI benchmark would begin by computing the LU decomposition of this matrix using 16-bit
half-precision floating point arithmetic, FP16. So, there is a signigant problem if the matrix order n is larger than 65504. This value is realmax, the largest number that can be represented in FP16. Any larger value of n overflows to Inf.
Some kind of scaling is going to have to be done for n > 65504. Right now, I don't see what this might be.
The alternative half-precision format to FP16 is Bfloat16, which has three more bits in the exponent to give realmax = 3.39e38. There should be no overflow problems while generating this matrix with Bfloat16.
Thanks
Thanks to Piotr Luszczek for working with me on this. We have more work to do.