这是设置。我使用的值没有任何假设。
n=2; % dimension of vectors x and (square) matrix P r=2; % number of x vectors and P matrices x1 = [3;5] x2 = [9;6] x = cat(2,x1,x2) P1 = [6,11;15,-1] P2 = [2,21;-2,3] P(:,1)=P1(:) P(:,2)=P2(:) modePr = [-.4;16] TransPr=[5.9,0.1;20.2,-4.8] pred_modePr = TransPr'*modePr MixPr = TransPr.*(modePr*(pred_modePr.^(-1))') x0 = x*MixPr 然后是时候应用以下公式来获取myP
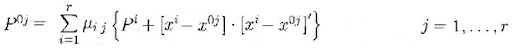
,其中ijij是MixPr。我使用以下代码来获取它:
myP=zeros(n*n,r); Ptables(:,:,1)=P1; Ptables(:,:,2)=P2; for j=1:r for i = 1:r; temp = MixPr(i,j)*(Ptables(:,:,i) + ... (x(:,i)-x0(:,j))*(x(:,i)-x0(:,j))'); myP(:,j)= myP(:,j) + temp(:); end end 一位有才华的人提出此公式作为产生myP另一种方法
for j=1:r xk1=x(:,j); PP=xk1*xk1'; PP0(:,j)=PP(:); xk1=x0(:,j); PP=xk1*xk1'; PP1(:,j)=PP(:); end myP = (P+PP0)*MixPr-PP1 我试图制定两种方法之间的相等性,似乎就是这种方法。为了使事情变得容易,我在两种方法中都跳过了矩阵P的求和。
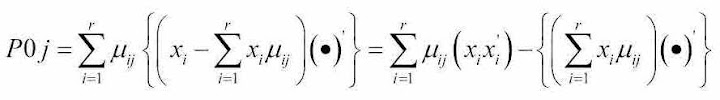
其中第一部分表示我使用的公式,第二部分来自他的代码段。您认为这是显而易见的平等吗?如果是,请忽略以上所有内容,然后尝试解释原因。我只能从LHS开始,经过一些代数后,我认为我证明它等于RHS。但是我看不出他(或她)最初是怎么想的。
回答:
使用E进行期望,公式的一维版本很常见:
Variance(X) = E((XE(X))^2) = E(X^2) - E(X)^2 尽管第二种形式可能更容易编程,但由于舍入误差,我担心会因使用否定(或者在多维情况下为非肯定的)而结束。
更多&回答...