事先有点冗长,我深表歉意:如果您想跳过所有背景知识,可以在下面看到我的问题。
这几乎是我先前发布的有关如何比较两个一维(随时间变化)信号的问题的跟进。我得到的答案之一是使用互相关函数(MATLAB中的xcorr)。
背景资料
也许一些背景信息会有用:我正在尝试实现独立组件分析算法。我的非正式测试之一是(1)通过(a)生成2个随机向量(1x1000)创建测试用例,(b)将向量合并成2x1000矩阵(称为“ S”),然后将其乘以2x2混合矩阵(称为“ A”),给我一个新的矩阵(我们称其为“ T”)。
总结:T = A * S
(2)然后运行ICA算法以生成混合矩阵的逆矩阵(称为“ W”),(3)将“ T”乘以“ W”,以(希望)为我重构原始信号矩阵(称为“X”)
总结:X = W * T
(4)我现在要比较“ S”和“ X”。尽管“ S”和“ X”为2x1000,但我只是将S(1,:)与X(1,:)以及S(2,:)与X(2,:) ,每个都是1x1000,从而使它们成为1D信号。 (我还有另外一个步骤,可以确保这些向量是相互比较的正确向量,并且还对信号进行了归一化处理)。
所以,我现在的困惑是如何'级'的接近S(1,:)火柴X(1,:) ,并同样与S(2,:)到X(2,:) 。
到目前为止,我已经使用过类似的东西: r1 = max(abs(xcorr(S(1,:), X(1,:)))
我的问题
假设使用互相关函数是比较两个信号相似度的一种有效方法,那么对信号相似度进行等级评定会被认为是一个好的R值吗? Wikipedia指出,这是一个非常主观的领域,因此,我谨请那些可能在该领域有经验的人做出更好的判断。
正如您可能意识到的那样,我根本不是来自EE / DSP /统计领域(我是医学生),所以我现在正在经历一种“洗礼受洗”,我非常感谢帮我得到。谢谢!
回答:
(
编辑:就直接回答有关R值的问题而言,请参见下文)
解决此问题的一种方法是使用互相关。请记住,您必须归一化幅度并校正延迟:如果信号S1和信号S2的形状相同,但是幅度的一半且延迟3个样本,则它们仍然是完美相关的。
例如:
>> t = 0:0.001:1; >> y = @(t) sin(10*t).*exp(-10*t).*(t > 0); >> S1 = y(t); >> S2 = 0.4*y(t-0.1); >> plot(t,S1,t,S2);
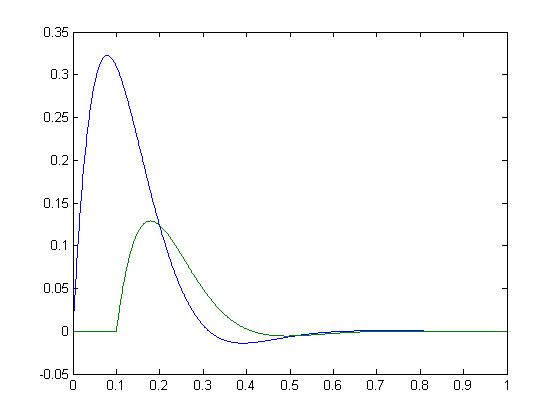
这些应该具有完美的相关系数。一种计算方法是使用最大互相关:
>> f = @(S1,S2) max(xcorr(S1,S2)); f = @(S1,S2) max(xcorr(S1,S2)) >> disp(f(S1,S1)); disp(f(S2,S2)); disp(f(S1,S2)); 12.5000 2.0000 5.0000 xcorr()的最大值负责信号之间的时间延迟。就幅度校正而言,您可以将信号归一化,以使它们的自互相关为1.0,或者可以将该等效步长折叠为以下内容:
ρ2 = F(S1,S2)2 /(F(S1,S1)* F(S2,S2);
在这种情况下ρ2 = 5×5 /(12.5 * 2)= 1.0
您可以求解ρ本身,即ρ= f(S1,S2)/ sqrt(f(S1,S1)* f(S2,S2)),只需记住1.0和-1.0都是完美相关的(-1.0有相反的符号)
试试看您的信号!
关于接受/拒绝使用的阈值,这实际上取决于您拥有哪种信号。 0.9及更高版本是不错的选择,但可能会引起误解。我会考虑查看减去相关版本后得到的残差信号。您可以通过查看xcorr()最大值的时间索引来做到这一点:
>> t = 0:0.001:1; >> y = @(a,t) sin(a*t).*exp(-a*t).*(t > 0); >> S1=y(10,t); >> S2=0.4*y(9,t-0.1); >> f(S1,S2)/sqrt(f(S1,S1)*f(S2,S2)) ans = 0.9959 对于关联而言,这看起来不错。但是,让我们尝试使用S1的缩放/移位倍数来拟合S2:
>> [A,i]=max(xcorr(S1,S2)); tshift = i-length(S1); >> S2fit = zeros(size(S2)); S2fit(1-tshift:end) = A/f(S1,S1)*S1(1:end+tshift); >> plot(t,[S2; S2fit]); % fit S2 using S1 as a basis

>> plot(t,[S2-S2fit]); % residual

残留物有一些能量;要了解多少,可以使用以下方法:
>> S2res=S2-S2fit; >> dot(S2res,S2res)/dot(S2,S2) ans = 0.0081 >> sqrt(dot(S2res,S2res)/dot(S2,S2)) ans = 0.0900 这表示残差具有原始信号S2能量的约0.81%(均方根振幅的9%)。 (一维信号与其自身的点积将始终等于该信号与自身的互相关的最大值。)
我认为,回答两个信号之间的相似程度不是灵丹妙药,但希望我给了您一些可能适合您的情况的想法。
更多&回答...