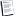[klmcrazy]

本文提出的利用小波域结构相似性灰关联对图像增强算法的基本思路如图2，即：首先对图像进行多层小波分解，如三层“sym8”小波分解，得到三个层次下三个不同方向的小波子图和最高层次下的概貌子图，然后对各子图中的系数分别进行如图2虚线框内的处理；最后，将处理后的各小波系数重构为增强图像。

图2 基于小波域结构相似性灰关联的强噪声图像增强算法示意图
具体实现步骤如下：
Step1. 读入图像，进行三层“sym8”小波分解，得到低频分量 、水平高频 、竖直高频 、对角高频 ，其中 =1,2,3。
Step2. 对小波域的水平高频系数进行噪声抑制和边缘增强处理，方法如下：
1 根据2.2小节的分析，经过三层小波分解得到的三个层次的水平高频子图图像均反映图像中水平信息特征，具有结构相似性；在小波域中 含噪声最少，其次分别为 和 。因此，可通过三者间的灰色关联度来区分某子图系数是噪声点还是边缘点，方法为：
设待判断的点为 ，则以其在三层水平高频系数 中的某小邻域(如图3(a)所示)形成参考序列 ，其在一层水平高频系数 和二层水平高频系数 中的对应小邻域分别形成比较序列 和 。为保证不同层次下的小波系数在进行灰关联时具有相同的维数，应对 和 分别进行插值预处理(本文采用最近邻插值法)，则：



其中： 为第一层水平高频子图图像的高和长。

(a) (b) (c)
图3 参考序列和比较序列选取示意图
2 根据式(1)、(2)分别计算出 和 的关联度 ， 和 的关联度 ，则增强后的第一层小波系数为
(3)
第二层的小波系数为
(4)
考虑到强噪声环境下，第三层小波系数中也会有小部分噪声，即参考序列非标准的无噪声序列，因此，当 和 均小于其对应的关联阈值时，也应对其进行抑制，否则进行增强，即
(5)
其中:
Step3. 对小波域的竖直高频系数进行增强处理；
处理方法与水平高频类似，区别在于竖直高频方向参考序列和比较序列的形成方式，其形成方式如图3(b)。
Step4. 对小波域的对角高频系数进行增强处理；
与水平高频系数和竖直高频系数不同， 点的关联度由与水平方向成45度夹角和135度夹角分别形成的参考序列和比较序列计算出的关联度的算术平均值确定。两组参考序列和比较序列的形成方式如图3(c)。
Step5. 先对增强后的第二层，第三层高频系数进行下采样，恢复到原始的维数。
Step6. 对增强后的小波系数进行小波逆变换，得到增强图像。